Heron-Verfahren (for-Schleife)

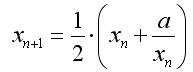
Mit Hilfe des Heron-Verfahrens kann man die Quadratwurzel einer Zahl a näherungsweise bestimmen. Die Zahl a, aus der die Wurzel gezogen wird, nennt man Radikand.

Die Zuordnungsvorschrift lautet:

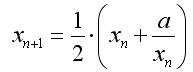
In diesem Beispiel kann man die n-te Näherung der Quadratwurzel von a ausgehend von einem Startwert bestimmen. Zum Vergleich wird die Quadratwurzel ausgegeben, die man mit Math.Sqrt bestimmen kann.

Normalerweise führt man Näherungsverfahren solange durch, bis eine gewünschte Genauigkeit erreicht ist. Dies macht aber das Beispiel etwas komplizierter, weshalb hier darauf verzichtet wird. Außerdem fehlen im unten dargestellten Quelltext alle Sicherheitsabfragen, die im Beispielprogramm eingebaut sind.

Quelltext: Ereignisbehandlung des Buttons

  protected void ButtonHeron_Click(object sender, EventArgs e)
  {
    // Listbox löschen
    ListBox1.Items.Clear();

    // Werte aus den Textboxes einlesen
    double a = double.Parse(TextBoxRadikand.Text);  // Radikand
    double xn = double.Parse(TextBoxStartwert.Text);  // Startwert
    int n = int.Parse(TextBoxNaeherung.Text); // Näherungsschritt

    // Startwert eintragen (ToString ist in Windows-Anwendungen unnötig)
    ListBox1.Items.Add(xn.ToString());

    // Heron-Verfahren anwenden
    for (int i = 1; i <= n; i++)
    {
      // nächste Näherung bestimmen
      xn = 0.5 * (xn + a / xn);
      // Ergebnis ausgeben
      ListBox1.Items.Add(xn.ToString());
    }

    // Vergleichswert berechen und ausgeben
    double vergleich = Math.Sqrt(a);
    LabelSqrt.Text = vergleich.ToString();
  }